刷题日记 - 11
难度:中等
二叉树 中序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class BSTIterator {
List<Integer> array;
int p;
int size;
public BSTIterator(TreeNode root) {
p = 0;
array = new ArrayList<>();
dfs(root);
size = array.size();
}
public int next() {
return array.get(p++);
}
public boolean hasNext() {
if(p < size) return true;
return false;
}
private void dfs(TreeNode node){
if(node == null) return;
dfs(node.left);
array.add(node.val);
dfs(node.right);
}
}
|
实现一个二叉树中序迭代器,我的思路是在初始化的时候就将先中序遍历的结果存入数组,然后根据指针来判断。
但是这个方法无论如何都会先中序遍历一边二叉树,这其实是没必要的,因为这个迭代器又不能回到上一个,把中序遍历的结果存入数组其实很没必要。
本题应该希望我们用栈来模拟中序遍历。
用栈模拟
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class BSTIterator {
Stack<TreeNode> stack;
public BSTIterator(TreeNode root) {
stack = new Stack<>();
if (root != null) stack.push(root);
while (!stack.isEmpty() && stack.peek().left != null) {
stack.push(stack.peek().left);
}
}
public int next() {
TreeNode node = stack.pop();
if (node.right != null) {
stack.push(node.right);
while (stack.peek().left != null) {
stack.push(stack.peek().left);
}
}
return node.val;
}
public boolean hasNext() {
return !stack.isEmpty();
}
}
|
可以回顾一下用栈完成二叉树的中序遍历。
难度:简单
二叉树
1
2
3
4
5
6
| class Solution {
public int countNodes(TreeNode root) {
if(root == null) return 0;
return countNodes(root.left) + countNodes(root.right) + 1;
}
}
|
可以直接遍历得到,时间复杂度O(n)。
但是没有利用到完全二叉树的特性。
如果要利用到完全二叉树的性质。
可以判断根节点的左子树和右子树哪一个是满二叉树,对于是满二叉树的子树,这一部分的节点数计算可以不用通过遍历计数。
如何判断呢?
- 左子树和右子树都是完全二叉树
- 完全二叉树的深度可以直接通过一直访问左节点得到
- 完全二叉树最后一层的节点是从左到右排列的
- 如果左子树和右子树深度相同,证明左子树是满二叉树 (有可能右子树也是满二叉树,这里也可以通过一直访问右节点来判断右子树是不是满二叉树)
- 如果深度不同,则右子树是满二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution {
public int countNodes(TreeNode root) {
if(root == null) return 0;
int res = 1;
int leftDepth = countLevel(root.left);
int rightDepth = countLevel(root.right);
if(leftDepth==rightDepth){
int leftCount = (int)Math.pow(2,leftDepth) - 1;
int rightCount = dfsCount(root.right);
res = res + leftCount + rightCount;
}else{
int leftCount = dfsCount(root.left);
int rightCount = (int)Math.pow(2,rightDepth) - 1;
res = res + leftCount + rightCount;
}
return res;
}
public int dfsCount(TreeNode node){
if(node==null)return 0;
return dfsCount(node.left)+dfsCount(node.right)+1;
}
public int countLevel(TreeNode node){
int count = 0;
while(node!=null){
count++;
node = node.left;
}
return count;
}
}
|
难度:中等
二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
return dfs(root, p, q);
}
private TreeNode dfs(TreeNode node, TreeNode p, TreeNode q) {
if (node == null || node == q || node == p) return node;
TreeNode l = dfs(node.left, p, q);
TreeNode r = dfs(node.right, p, q);
if (l == null) return r;
if (r == null) return l;
return node;
}
}
|
dfs函数只会返回3个值:
dfs先序遍历遇到p或者q节点之后就会往回回溯。
如果对于某一个节点l和r都不为null表明它就是最近共公父节点。
如果对于某一个节点l的值为null,r不为null,那么证明两个节点一定在该节点的右节点。
l!=null, r==null同理。
当l,r都为null,则表示目标节点都不在这颗节点之下。
难度:简单
二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public List<Double> averageOfLevels(TreeNode root) {
List<Double> res = new ArrayList<>();
if(root==null)return res;
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offerLast(root);
queue.offerLast(null);
double sum = 0;
int count = 0;
while(true){
TreeNode cur = queue.pollFirst();
if(cur!=null){
count++;
sum += cur.val*1.0;
if(cur.left!=null)queue.offerLast(cur.left);
if(cur.right!=null)queue.offerLast(cur.right);
}else{
res.add(sum/count);
sum = 0;
count = 0;
if(queue.isEmpty())break;
queue.offerLast(null);
}
}
return res;
}
}
|
就是二叉树层序遍历。
难度:中等
二叉树 链表头插
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if(root==null)return res;
boolean LEFT = true;
boolean RIGHT = false;
LinkedList<TreeNode> queue = new LinkedList<>();
queue.offerLast(root);
queue.offerLast(null);
boolean STATE = RIGHT;
List<Integer> tmp = new LinkedList<>();
while(true){
TreeNode cur = queue.pollFirst();
if(cur!=null){
if(STATE==LEFT){
tmp.add(0,cur.val);
}else{
tmp.add(cur.val);
}
if(cur.left!=null)queue.offerLast(cur.left);
if(cur.right!=null)queue.offerLast(cur.right);
}else{
res.add(tmp);
tmp = new ArrayList<>();
STATE = STATE==LEFT?RIGHT:LEFT;
if(queue.isEmpty())break;
queue.offerLast(null);
}
}
return res;
}
}
|
难度:中等
分区动态规划 字符串
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| class Solution {
public int minimumSubstringsInPartition(String s) {
char[] chars = s.toCharArray();
int len = chars.length;
boolean[][] map = new boolean[len][len];
int[] counter = new int[26];
for(int i=0;i<len;i++){
Arrays.fill(map[i],true);
Arrays.fill(counter,0);
counter[chars[i]-'a']++;
for(int j=i+1;j<len;j++){
counter[chars[j]-'a']++;
int tmp = -1;
for(int count:counter){
if(count>0){
if(tmp==-1)tmp = count;
if(count!=tmp){
map[i][j] = false;
break;
}
}
}
}
}
int[] dp = new int[len];
for(int i=0;i<len;i++){
if(map[0][i])dp[i]=1;
else{
int min = Integer.MAX_VALUE;
for(int j=1;j<=i;j++){
if(map[j][i]){
min = Math.min(min,dp[j-1]);
}
}
dp[i] = min+1;
}
}
return dp[len-1];
}
}
|
时间复杂度O(n^2^)
给map赋值那一段可以进行优化,不必每次都遍历一次counter数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
for(int i=0;i<len;i++){
Arrays.fill(map[i],true);
Arrays.fill(counter,0);
counter[chars[i]-'a']++;
int count = 1;
int max = 1;
for(int j=i+1;j<len;j++){
if(counter[chars[j]-'a']==0)count++;
counter[chars[j]-'a']++;
max = Math.max(counter[chars[j]-'a'],max);
if(j-i+1!=count*max)map[i][j] = false;
}
}
|
记录i->j中有多少种字符,以及字符出现的最大次数,如果总字符串不等于字符种类数*字符出现最大次数,那么直接判定该子串不是平衡子串。
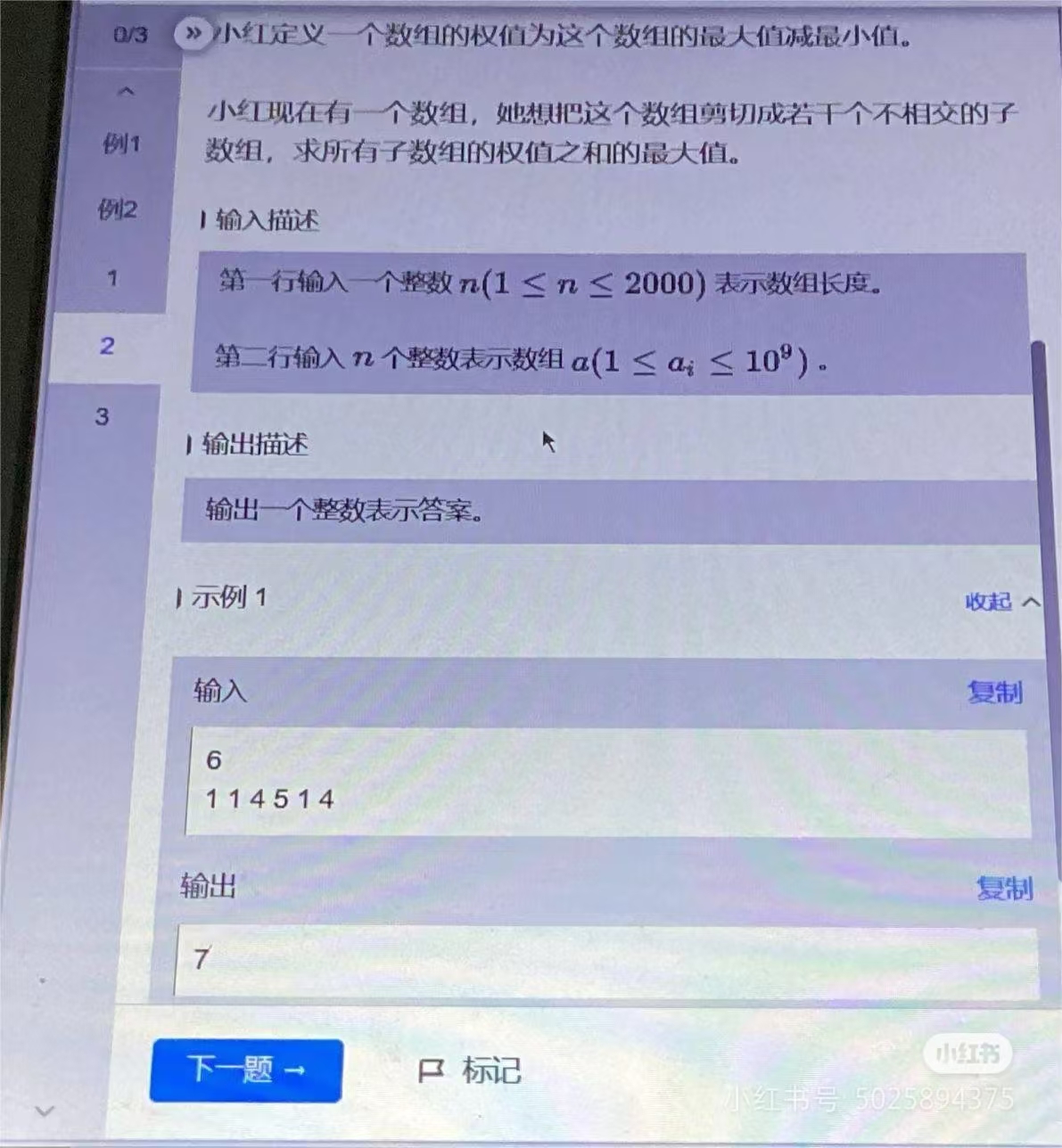
饿了么 8-23 笔试第二题
动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
public class Helloworld {
public static void main(String[] args) {
int[] arr = {1,1,4,5,1,4,1,2,3,4,1,3,5,6,7,1,2,3,6};
int n = arr.length;
long[] dp = new long[n + 1];
int MAX = 1_000_000_001;
for (int i = 0; i < n; i++) {
int max = 0, min = MAX;
for (int j = i; j < n; j++) {
max = Math.max(arr[j], max);
min = Math.min(arr[j], min);
dp[j + 1] = Math.max(dp[j + 1], max - min + dp[i]);
}
}
System.out.println(dp[n]);
}
}
|
难度:中等
字符串 dfs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
List<String> res = new ArrayList<>();
public List<String> restoreIpAddresses(String s) {
char[] chars = s.toCharArray();
int len = chars.length;
LinkedList<Integer> list = new LinkedList<>();
dfs(chars,0,len,list);
return res;
}
private void dfs(char[] chars,int cur,int len,LinkedList<Integer> list){
if(list.size()==4&&cur==len){
StringBuilder sb = new StringBuilder();
sb.append(list.get(0));
sb.append('.');
sb.append(list.get(1));
sb.append('.');
sb.append(list.get(2));
sb.append('.');
sb.append(list.get(3));
res.add(sb.toString());
}else if(list.size()==4&&cur<len)return;
int val = 0;
for(int i=cur;i<len;i++){
int curElem = chars[i] - '0';
val = val*10 + curElem;
if(val<=255){
list.offerLast(val);
dfs(chars,i+1,len,list);
list.pollLast();
}
if(val==0||val>255)break;
}
}
}
|
将IP地址转换为int,再将int转换为IP地址
int占4个字节,IP地址是String,占用的空间7-15个字节。
这样做可以节省空间,IP地址正好是四个八位二进制数,所以正好可以用int表示。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| public class Test {
public static void main(String[] args) {
String ip = "192.168.0.1";
int res = IP2Int(ip);
System.out.println(res);
String a = Int2IP(res);
System.out.println(a);
}
private static int IP2Int(String ip){
String[] strs = ip.split("\\.");
int res = 0;
for(int i=0;i< strs.length;i++){
int pos = 8*(3-i);
int val = Integer.parseInt(strs[i]) << pos;
res = res|val;
}
return res;
}
private static String Int2IP(int IPint){
String[] strs = new String[4];
for(int i=0;i<4;i++){
int pos = (3-i)*8;
int tmp = IPint & (255 << pos);
int val = tmp >>> pos;
strs[i] = String.valueOf(val);
}
return String.join(".",strs);
}
}
|
利用位运算,将IP的四个部分分布在32位中的四个8位,然后组合成一个整数。
注意,最后往右移的时候,是无符号右移。
>> 算术右移,如果是正数左边用0填充,如果左边是负数用1填充
>>>逻辑右移,全用0填充
