基础算法 - 栈
在计算机科学中,数据结构是算法和程序设计的基石。栈(Stack)作为其中一种重要的数据结构,以其独特的“后进先出”(Last In First Out, LIFO)特性,在各种应用中扮演着关键角色。从函数调用栈到表达式求值,栈的应用无处不在。
在开始之前,我们先来回顾一下栈的定义和特点。栈是一种线性数据结构,具有以下两个主要操作:
- 压栈(Push):将元素添加到栈的顶端。
- 弹栈(Pop):移除并返回栈顶元素。
通过这些基本操作,栈能够高效地管理数据的存取顺序。接下来,我们将详细介绍栈的实现方法和应用场景。
此篇记录使用栈解题的思路。
相关题目
难度:简单
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public boolean isValid(String s) {
LinkedList<Character> stack = new LinkedList<>();
char[] sChars = s.toCharArray();
for(char ch: sChars){
if(stack.isEmpty()){
if(ch==')'||ch==']'||ch=='}')
return false;
else
stack.push(ch);
}else{
char peek = stack.peek();
if(ch==')'&&peek=='(')
stack.pop();
else if(ch==']'&&peek=='[')
stack.pop();
else if(ch=='}'&&peek=='{')
stack.pop();
else stack.push(ch);
}
}
if(stack.isEmpty())
return true;
else return false;
}
}
|
为什么使用栈?
栈的特点使得它非常适合处理成对出现的匹配问题。具体来说:
- 后进先出(LIFO):当我们遇到一个闭括号时,我们需要检查最近的一个开括号是否与之匹配。这正是栈的后进先出性质能够完美实现的功能。我们可以通过弹出栈顶元素来检查匹配情况。
- 开括号和闭括号的顺序:栈能帮助我们记录未匹配的开括号,当遇到闭括号时,直接检查栈顶的开括号是否匹配。如果匹配,则弹出栈顶元素,表示这一对括号已经匹配。
难度:中等
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class MinStack {
LinkedList<Integer> stack;
LinkedList<Integer> min;
public MinStack() {
stack = new LinkedList<>();
min = new LinkedList<>();
}
public void push(int val) {
stack.push(val);
if(min.isEmpty()){
min.push(val);
}else{
int peek = min.peek();
if(peek<val){
min.push(peek);
}else{
min.push(val);
}
}
}
public void pop() {
stack.pop();
min.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return min.peek();
}
}
|
为了在常数时间内获取最小值,我们引入了一个辅助栈 min。辅助栈 min 的每个元素对应于主栈 stack 中的元素,使得 min 栈顶始终保持当前栈的最小值。因此,通过同步更新 min 栈,我们可以在 O(1) 时间复杂度内获取栈中的最小值。
难度:中等(中等偏上)
嵌套括号是本题的难点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
LinkedList<String> Sstack;
LinkedList<Integer> Istack;
String tmp = "";
int k = 0;
public String decodeString(String s) {
Sstack = new LinkedList<>();
Istack = new LinkedList<>();
for (char ch : s.toCharArray()) {
if (Character.isDigit(ch)) {
k = k * 10 + ch - '0';
} else if (ch == '[') {
Istack.push(k);
k = 0;
Sstack.push(tmp);
tmp = "";
} else if (ch == ']') {
StringBuffer sb = new StringBuffer(Sstack.pop());
int times = Istack.pop();
for (int i = 0; i < times; i++) {
sb.append(tmp);
}
tmp = sb.toString();
} else {
tmp += ch;
}
}
return tmp;
}
}
|

为什么用栈
在处理嵌套的结构(如括号中的括号)时,栈是一种非常自然且有效的数据结构。对于这道题目,使用栈的关键作用如下:
- 处理嵌套结构:栈的后进先出(LIFO)特性非常适合处理嵌套的括号结构。在遇到
[ 时,我们将当前的状态(当前字符串和当前的数字)入栈,以便在遇到 ] 时能够恢复并继续处理。
- 保存状态:当遇到
[ 时,我们需要保存当前的字符串和倍数,因为接下来的内容是一个新的子字符串,直到遇到对应的 ] 才会结束。使用栈可以方便地保存和恢复这些状态。
- 简化操作:通过栈,我们可以很方便地进行字符串的累积和倍数的计算,不需要额外的复杂数据结构或逻辑。
难度:中等
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int len = temperatures.length;
int[] res = new int[len];
LinkedList<Integer> stack = new LinkedList<>();
int p = 0;
while(p<len){
if(stack.isEmpty()){
stack.push(p);
p++;
}else{
if(temperatures[stack.peek()]>=temperatures[p]) {
stack.push(p);
p++;
}else{
while (!stack.isEmpty()&&temperatures[stack.peek()]<temperatures[p]){
int tmp = stack.pop();
res[tmp] = p-tmp;
}
}
}
}
return res;
}
}
|
这个题挺简单的,就是利用栈的特性,维护一个从栈底到栈顶是 大->小的顺序,如果新来的下一个元素比当前的栈顶大,那么就依次pop,pop的同时更新res数组,因为这个新来的大元素就是栈中小元素的”下一个”大元素。
为了方便起见,我们在栈中存放的是index
难度:简单
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
LinkedList<Integer> stack = new LinkedList<>();
int[] help = new int[10001];
for(int i=0;i<nums2.length;i++){
if(!stack.isEmpty()){
int peek = stack.peek();
while(peek<nums2[i]){
help[stack.pop()] = nums2[i];
if(stack.isEmpty()) break;
peek = stack.peek();
}
}
stack.push(nums2[i]);
}
int[] res = new int[nums1.length];
for(int i=0;i<nums1.length;i++){
res[i] = (help[nums1[i]]==0)?-1:help[nums1[i]];
}
return res;
}
}
|
这一题与 [每日温度](#739. 每日温度 - 力扣(LeetCode)) 很像,都是通过维护单调栈得到下一个更大的元素的值或者下标。
难度:中等
与 [下一个更大元素 Ⅰ](#496. 下一个更大元素 I - 力扣(LeetCode)) 相比,这里的数组是循环数组,这意味着最后一个元素的下一个是第一个元素。所以,进行两次数组的出栈入栈操作即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public int[] nextGreaterElements(int[] nums) {
int n = nums.length;
int[] result = new int[n];
Arrays.fill(result, -1);
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < n; i++) {
while (!stack.isEmpty() && nums[stack.peek()] < nums[i]) {
result[stack.pop()] = nums[i];
}
stack.push(i);
}
for (int i = 0; i < n; i++) {
while (!stack.isEmpty() && nums[stack.peek()] < nums[i]) {
result[stack.pop()] = nums[i];
}
}
return result;
}
}
|
难度:中等
这个题与栈没关系了。更像 [下一个排列](#31. 下一个排列 - 力扣(LeetCode))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public int nextGreaterElement(int n) {
char[] con = Integer.toString(n).toCharArray();
int len = con.length;
int p = len-1;
for(;p>=1;p--){
if(con[p-1]<con[p])break;
}
if(p==0)return -1;
int q = len-1;
for(;q>=p;q--){
if(con[q]>con[p-1])break;
}
char tmp = con[q];
con[q] = con[p-1];
con[p-1] = tmp;
reverse(con,p,len-1);
System.out.println(Arrays.toString(con));
long ans = Long.parseLong(String.valueOf(con));
if(ans>Integer.MAX_VALUE) return -1;
return (int)ans;
}
private void reverse(char[] con,int start,int end){
for(int i=start,j=end;i<j;i++,j--){
char tmp = con[i];
con[i] = con[j];
con[j] = tmp;
}
}
}
|
数组 双指针
主要还是弄懂题目的解法步骤,如何去拆分成可以被程序表达的步骤

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public void nextPermutation(int[] nums) {
int len = nums.length;
int p = len-1;
for(;p>=1;p--){
if(nums[p-1]<nums[p])break;
}
if(p==0){
reverse(nums,0,len-1);
return;
}
int q=len-1;
for(;q>p-1;q--){
if(nums[p-1]<nums[q])break;
}
int tmp = nums[p-1];
nums[p-1] = nums[q];
nums[q] = tmp;
reverse(nums,p,len-1);
return;
}
private void reverse(int[] nums,int start,int end){
for(int i=start,j=end;i<j;i++,j--){
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
}
|
难度:困难
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
public int largestRectangleArea(int[] heights) {
LinkedList<Integer> stack = new LinkedList<>();
stack.push(-1);
int res = Integer.MIN_VALUE;
for(int i=0;i<=heights.length;i++){
int cur;
if(i!=heights.length){
cur = heights[i];
}else{
cur = -1;
}
int peekIdx = stack.peek();
int peek;
if(peekIdx!=-1){
peek = heights[peekIdx];
}else{
peek = -1;
}
while(peek>cur){
stack.pop();
int h = peek;
int w = i - stack.peek() - 1;
res = Math.max(h*w,res);
peekIdx = stack.peek();
if(peekIdx!=-1){
peek = heights[peekIdx];
}else{
peek = -1;
}
}
stack.push(i);
}
return res;
}
}
|
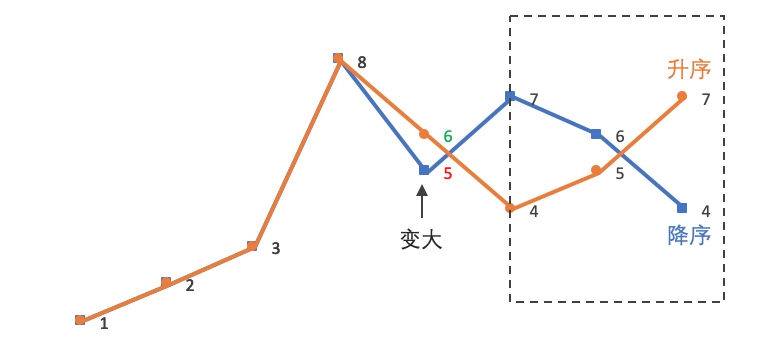
维护一个单调栈,栈底 << 栈顶,当有新的值要入栈时,如果新的值比当前栈顶的值小,那么就计算以当前栈顶高度为高的最大矩形面积,宽就为当前值的索引 减去 当前栈顶弹出后新栈顶的值(这个索引对应的高度一定小于当前栈顶,所以这里是这个高度所能向左边延申的边界) 再减 1
所以该题关键是找到某个高度能延申的左右边界,以高度为单位求最大矩形面积。
难度:中等
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public String removeDuplicateLetters(String s) {
int[] count = new int[26];
for (char ch : s.toCharArray()) {
count[ch - 'a']++;
}
boolean[] flag = new boolean[26];
LinkedList<Character> stack = new LinkedList<>();
for (char ch : s.toCharArray()) {
if (!flag[ch - 'a']) {
while (!stack.isEmpty() && stack.peek() > ch && count[stack.peek() - 'a'] > 0) {
flag[stack.pop() - 'a'] = false;
}
stack.push(ch);
flag[ch - 'a'] = true;
}
count[ch - 'a']--;
}
StringBuilder res = new StringBuilder();
while (!stack.isEmpty()) {
res.append(stack.removeLast());
}
return res.toString();
}
}
|
维护单调栈,但是这个题维护单调栈有一些额外的要求,比如说每个不同的字母只能出现一次(flag数组辅助),还要保证必须出现一次,即不能错过这个字母(count数组辅助)。
难度:中等
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
public String removeKdigits(String num, int k) {
int len = num.length();
if(k>=len)return "0";
LinkedList<Character> stack = new LinkedList<>();
int cnt = 0;
for(char ch : num.toCharArray()){
while(!stack.isEmpty()&&stack.peek()>ch&&cnt<k){
stack.pop();
cnt++;
}
stack.push(ch);
}
for(;cnt<k;cnt++){
stack.pop();
}
while(!stack.isEmpty()&&stack.getLast()=='0'){
stack.removeLast();
}
String res = "";
while(!stack.isEmpty()){
res += stack.removeLast();
}
return (res=="")?"0":res;
}
}
|
用数组模拟栈,stack中存放索引,这样可以使得代码运行更快。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public String removeKdigits(String num, int k) {
int len = num.length();
if(k>=len)return "0";
int[] stack = new int[len];
int top = -1;
char[] con = num.toCharArray();
for(int i=0;i<len;i++){
while(top!=-1&&con[stack[top]]>con[i]&&k>0){
k--;
top--;
}
top++;
stack[top] = i;
}
top -= k;
int start = 0;
for(;start<=top;start++){
if(con[stack[start]]=='0')
continue;
else
break;
}
if(start>top)
return "0";
StringBuffer sb =new StringBuffer();
for(int i=start;i<=top;i++){
sb.append(con[stack[i]]);
}
return sb.toString();
}
}
|
该题也是在维护单调栈的同时要满足一些要求,比如说规定了从栈中pop出的元素的数量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
class Solution {
int[] res;
LinkedList<Integer> stack = new LinkedList<>();
public int[] nextLargerNodes(ListNode head) {
f(head,0);
return res;
}
private void f(ListNode p,int i){
if(p==null){
res = new int[i];
return;
}
f(p.next,i+1);
while(!stack.isEmpty()&&stack.peek()<=p.val){
stack.pop();
}
if(!stack.isEmpty()){
res[i] = stack.peek();
}
stack.push(p.val);
}
}
|
由于现在操作的目标是链表,无法获得其索引值,需要一些技巧初始化res,并且需要用合适的方式遍历链表 维护单调栈。
主要思路
- 递归到底,初始化结果数组:
- 使用递归遍历链表,直到链表的末尾。在到达末尾节点时,确定结果数组
res 的长度。
- 从后向前处理节点:
- 递归函数在递归到底返回时,从最后一个节点开始向前处理。这相当于反向遍历链表,方便我们使用栈来找到每个节点的下一个更大节点。
- 利用栈来找到下一个更大节点:
- 使用栈来存储节点值,保证栈中的元素是单调递减的,这样可以快速找到每个节点的下一个更大节点。
从前向后遍历维护单调栈 与 从后向前遍历维护单调栈 有什么不同?
前者确定下一个更大的元素是在 更大的元素加入栈后将小的元素依次pop出的时候确定的。
后者确定下一个更大的元素是在 将新元素与当前栈顶元素进行比较,将不行的pop出,直到找到大于当前新元素的栈顶,这时才能确定。
也就是说,前者可能出现新元素入栈时候确定了很多个元素的下一个最大元素,而后者是新元素入栈时只能确定新元素的下一个最大元素。


